CODE
% Let's start with a simple example.
data = randnmulti(100,[10 6],[1 .6; .6 1],[3 1]);
figure(999); clf; hold on;
scatter(data(:,1),data(:,2),'r.');
axis square; axis([0 20 0 20]);
set(gca,'XTick',0:1:20,'YTick',0:1:20);
xlabel('X'); ylabel('Y');
title('Data');

% To compute the correlation, let's first standardize each
% variable, i.e. subtract off the mean and divide by the
% standard deviation. This converts each variable into
% z-score units.
dataz = calczscore(data,1);
figure(998); clf; hold on;
scatter(dataz(:,1),dataz(:,2),'r.');
axis square; axis([-5 5 -5 5]);
set(gca,'XTick',-5:1:5,'YTick',-5:1:5);
xlabel('X (z-scored)'); ylabel('Y (z-scored)');

% We would like a single number that represents the relationship
% between X and Y. Points that lie in the upper-right or lower-left
% quadrants support a positive relationship between X and Y (i.e.
% higher on X is associated with higher on Y), whereas points that
% lie in the upper-left or lower-right quadrants support a negative
% relationship between X and Y (i.e. higher on X is associated with
% lower on Y).
set(straightline(0,'h','k-'),'Color',[.6 .6 .6]);
set(straightline(0,'v','k-'),'Color',[.6 .6 .6]);
text(4,4,'+','FontSize',48,'HorizontalAlignment','center');
text(-4,-4,'+','FontSize',48,'HorizontalAlignment','center');
text(4,-4,'-','FontSize',60,'HorizontalAlignment','center');
text(-4,4,'-','FontSize',60,'HorizontalAlignment','center');

% Let's calculate the "average" relationship. To do this, we compute
% the average product of the X and Y variables (in the z-scored space).
% The result is the correlation value.
r = mean(dataz(:,1) .* dataz(:,2));
title(sprintf('r = %.4g',r));

% Now, let's turn to a different (but in my opinion more useful)
% interpretation of correlation. Let's start with a simple example.
data = randnmulti(100,[10 6],[1 .8; .8 1],[3 1]);
% For each set of values, subtract off the mean and scale the values such
% that the the values have unit length (i.e. the sum of the squares of the
% values is 1).
datanorm = unitlength(zeromean(data,1),1);
% The idea is that each set of values represents a vector in a
% 100-dimensional space. After mean-subtraction and unit-length-normalization,
% the vectors lie on the unit sphere. The correlation is simply
% the dot-product between the two vectors. If the two vectors are
% very similar to one another, the dot-product will be high (close to 1);
% if the two vectors are not very similar to one another (think: randomly
% oriented), the dot-product will be low (close to 0); if the two vectors
% are very anti-similar to one another (think: pointing in opposite
% directions), the dot product will be very negative (close to -1).
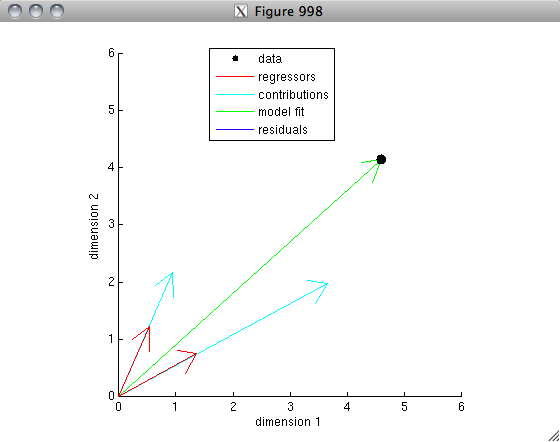
% Let's visualize this for our example.
% the idea here is to project the 100-dimensional space onto
% two dimensions so that we can actually visualize the data.
% the first dimension is simply the first vector.
% the second dimension is the component of the second vector that
% is orthogonal to the first vector.
dim1 = datanorm(:,1);
dim2 = unitlength(projectionmatrix(datanorm(:,1))*datanorm(:,2));
% compute the coordinates of the two vectors in this reduced space.
c1 = datanorm(:,1)'*[dim1 dim2];
c2 = datanorm(:,2)'*[dim1 dim2];
% make a figure
figure(997); clf; hold on;
axis square; axis([-1.2 1.2 -1.2 1.2]);
h1 = drawarrow([0 0; 0 0],[c1; c2],[],[],[],'LineWidth',4,'Color',[1 .8 .8]);
h2 = drawellipse(0,0,0,1,1,[],[],'k-');
h3 = plot([c2(1) c2(1)],[0 c2(2)],'k--');
h4 = plot([0 c2(1)],[0 0],'r-','LineWidth',4);
xlabel('Dimension 1');
ylabel('Dimension 2');
legend([h1(1) h2 h4],{'Data' 'Unit sphere' 'Projection'});
r = dot(datanorm(:,1),datanorm(:,2));
title(sprintf('r = %.4g',r));

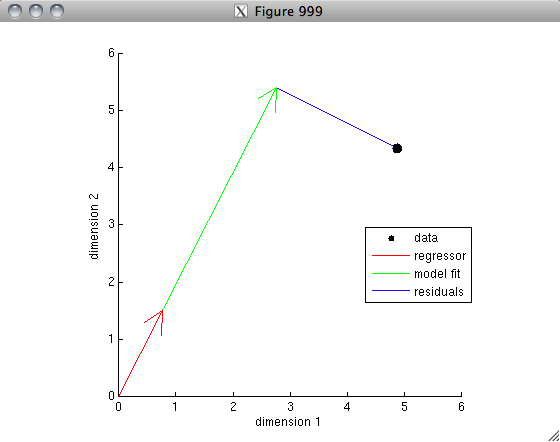
% The vector interpretation lends itself readily to the concept
% of variance explained. Suppose that we are using one vector A
% to predict the other vector B in a linear regression sense. Then,
% the weight applied to vector A is equal to the correlation
% value. (This is because inv(A'*A)*A'*B = inv(1)*A'*B = A'*B = r.)
% Let's visualize this.
figure(996); clf; hold on;
axis square; axis([-1.2 1.2 -1.2 1.2]);
h1 = drawarrow([0 0],c2,[],[],[],'LineWidth',4,'Color',[1 0 0]);
h2 = drawarrow([0 0],r*c1,[],[],[],'LineWidth',4,'Color',[0 1 0]);
h3 = plot([r r],[0 c2(2)],'b-');
h4 = drawellipse(0,0,0,1,1,[],[],'k-');
text(.3,.38,'1');
text(.35,-.1,'r');
xlabel('Dimension 1');
ylabel('Dimension 2');
legend([h1 h2 h3 h4],{'Vector B' 'Vector A (scaled by r)' 'Residuals' 'Unit sphere'});

% So, we ask, how much variance in vector B is explained by vector A?
% The total variance in vector B is 1^2. By the Pythagorean Theorem,
% the total variance in the residuals is 1^2 - r^2. So, the fraction
% of variance that we do not explain is (1^2 - r^2) / 1^2, and
% so the fraction of variance that we do explain is 1 - (1^2 - r^2) / 1^2,
% which simplifies to r^2. (Note that here, in order to keep things simple,
% we have invoked a version of variance that omits the division by the number
% of data points. Under this version of variance, the variance associated
% with a zero-mean vector is simply the sum of the squares of the elements
% of the vector, which is equivalent to the square of the vector's length.
% Thus, there is a nice equivalence between variance and squared distance,
% which we have exploited for our interpretation.)
FINAL REMARKS
There is much more to be said about correlation; we have covered here only the basics.
One important caveat to keep in mind is that correlation is not sensitive to offset and gain. This is because the mean of each set of numbers is subtracted off and because the scale of each set of numbers is normalized out. This has several consequences:
- Correlation indicates how well deviations relative to the mean can be predicted. This is natural, since variance (normally defined) is also relative to the mean.
- When using correlation as a index of how well one set of numbers predicts another set of numbers, you are implicitly allowing scale and offset parameters in your model. If you want to be completely parameter-free, you should instead use a metric like R^2 (which will be described in a later post).