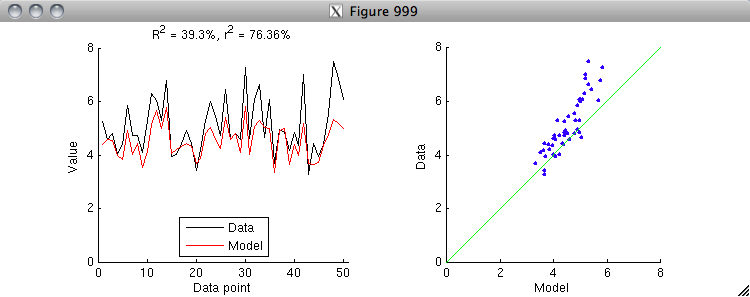
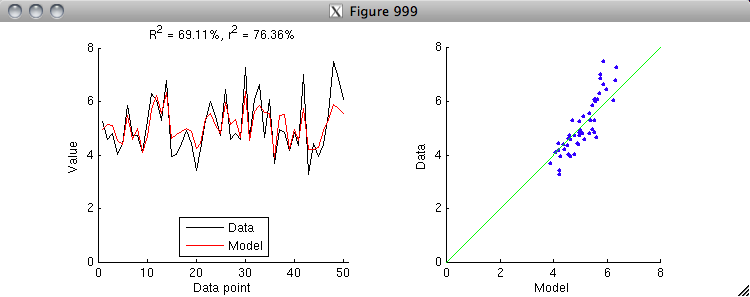
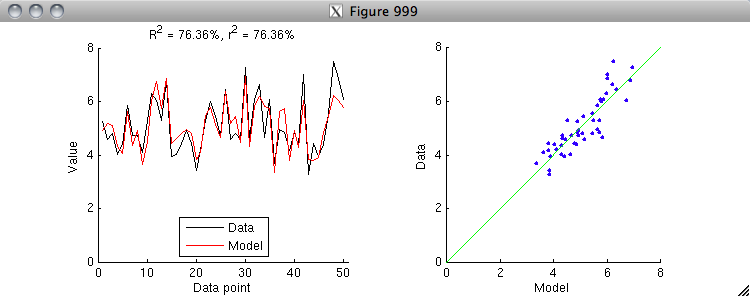
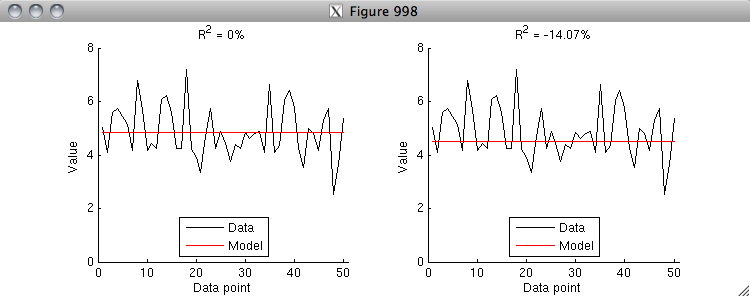
CODE
% Let's look at a basic probability distribution, the Gaussian
% distribution. In the one-dimensional case, there are two parameters,
% the mean and the standard deviation. Let's see an example.
mn = 3;
sd = 1;
fun = @(x) 1/(sd*sqrt(2*pi)) * exp(-(x-mn).^2/(2*sd^2));
% We have defined a function that takes a value and returns
% the corresponding likelihood for a Gaussian distribution with
% mean 3 and standard deviation 1. This function is called
% a probability density function. Let's visualize it.
figure(999); clf; hold on;
xx = -1:.01:7;
h1 = plot(xx,feval(fun,xx),'r-','LineWidth',2);
xlabel('Value');
ylabel('Likelihood');
legend(h1,{'Probability density function'});

% For a Gaussian distribution, about 95% of the time, values drawn
% from the distribution will lie within two standard deviations
% of the mean. In our example, this range is between 1 and 5.
xx2 = linspace(mn-2*sd,mn+2*sd,100);
h2 = bar(xx2,feval(fun,xx2),1);
set(h2,'FaceColor',[.8 .8 .8]);
set(h2,'EdgeColor','none');
uistack(h1,'top');

% We have shaded in the area underneath the probability density function
% that lies between 1 and 5. If we were to calculate the actual area
% of this region, we would find that it is (approximately) 0.95.
% The total area underneath the probability density function is 1.
delete(h2);
% Now let's consider the concept of calculating the likelihood of a
% set of data given a particular probability distribution. Using
% our example Gaussian distribution (mean 3, standard deviation 1),
% let's calculate the likelihood of a sample set of data.
data = [2.5 3 3.5];
h3 = straightline(data,'v','b-');
likelihood = prod(feval(fun,data));
legend([h1 h3(1)],{'Probability density function' 'Data points'});
title(sprintf('Likelihood of data points = %.6f',likelihood));

% The likelihood of observing the data points 2.5, 3, and 3.5 is
% obtained by multiplying the likelihoods of each individual data
% point. (We are assuming that the data points are independent.)
% Now, for comparison, let's calculate the likelihood of a different
% set of data.
delete(h3);
data = [4 4.5 5];
h3 = straightline(data,'v','b-');
likelihood = prod(feval(fun,data));
legend([h1 h3(1)],{'Probability density function' 'Data points'});
title(sprintf('Likelihood of data points = %.6f',likelihood));

% Notice that the likelihood of this new set of data is much smaller
% then that of the original set of data.
% Now that we know how to calculate the likelihood of a set of data
% given a particular probability distribution, we can now think about
% how to actually fit a probability distribution to a set of data.
% All that we need to do is to set the parameters of the probability
% distribution such that the likelihood of the set of data is maximized.
% Let's do an example. We have several data points and we want to fit
% a univariate (one-dimensional) Gaussian distribution to the data.
% To determine the optimal mean and standard deviation parameters,
% let's use brute force.
data = randn(1,100)*2.5 + 4;
fun = @(pp) sum(-log(1/(abs(pp(2))*sqrt(2*pi)) * exp(-(data-pp(1)).^2/(2*pp(2)^2))));
options = optimset('Display','iter','FunValCheck','on', ...
'MaxFunEvals',Inf,'MaxIter',Inf,'TolFun',1e-6,'TolX',1e-6);
params = fminsearch(fun,[0 1],options);
% What we have done is to use fminsearch to determine the mean and standard
% deviation parameters that minimize the sum of the negative log likelihoods
% of the data points. (Maximizing the product of the likelihoods of the data
% points is equivalent to maximizing the log of the product of the likelihoods
% of the data points, which is equivalent to maximizing the sum of the log of
% the likelihood of each data point, which is equivalent to minimizing the
% sum of the negative log likelihood of the data points. Or, semi-formally:
% Let <ps> be a vector of likelihoods. Then,
% max prod(ps) <=> max log(prod(ps))
% <=> max sum(log(ps))
% <=> min sum(-log(ps))
% Note that taking the log of the likelihoods helps avoid numerical
% precision issues.) Let's visualize the results.
mn = params(1);
sd = abs(params(2));
fun = @(x) 1/(sd*sqrt(2*pi)) * exp(-(x-mn).^2/(2*sd^2));
figure(998); clf; hold on;
h2 = straightline(data,'v','k-');
ax = axis;
xx = linspace(ax(1),ax(2),100);
h1 = plot(xx,feval(fun,xx),'r-','LineWidth',2);
axis([ax(1:2) 0 max(feval(fun,xx))*1.1]);
xlabel('Value');
ylabel('Likelihood');
legend([h2(1) h1],{'Data' 'Model'});

% Let's take the mean and standard deviation parameters that we found
% using optimization and compare them to the mean and standard deviation
% of the data points.
params
[mean(data) std(data,1)]

% Notice that the two sets of results are more or less identical (the
% difference can be attributed to numerical precision issues). Thus,
% we see that computing the mean and standard deviation of a set of
% data can be viewed as implicitly fitting a one-dimensional
% Gaussian distribution to the data.